この記事の見出し
はじめに
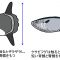
非対称単純排他過程(ASEP)とは図1に示すような、一次元の格子点の上を粒子が流れていく確率過程で、同じ場所(サイト)には最大一つしか粒子が入ることできないという制約条件がある非対称なランダムウォークのことを言います。この確率過程は非平衡物理学の文脈で(厳密に解が求まったり、非平衡な相転移が起こったりという様々な理由で)長らく研究されてきました。一方、「ながれ」を記述する非常に単純な数理モデルとしても活用され、車の渋滞や、蟻の移動、細胞内モーターたんぱく質の輸送現象を記述・説明するのに利用されています。
このASEPに対しては様々な拡張が行われていて、例えばレーンの数を増やしたり、レーンの途中で粒子が脱着出来たり、といったルールを追加した系の振る舞いを調べるということも盛んにおこなわれてきました。こうした拡張は上記の現象の数理モデルとしてのASEPにとって非常に重要な意味を持ちます。

図1. ASEP. 粒子は次のサイトが空いていれば一定の確率レートで移動するが,前のサイトが別の粒子によって占有されている場合は動くことができない.
“厳密解”について
一般に、数理の視点からは、作った数理モデルは数学的に「解ける」ととてもうれしいです。モデルの「解」が見つかると、複雑な計算やシミュレーションをしなくてもそのシステムの振る舞いを数式から直接知ることができるからです。(最終的に得られた数式が扱いやすいかどうかというのはまた別の問題ですが…)ASEPのような確率モデルの解は普通、「ある状態がどれくらいの確率で発生するか」をすべてのあり得る場合について計算しきれればそれが「解けた」という状態になります。その確率から例えば「平均的にはどれくらいの粒子が流れるか」といった量(期待値)を計算することできます。ASEPについてはその解が知られています。このモデルは非常に単純ながら、同じサイトに粒子が二つ以上入ることができないという制約がなかなか厄介で、これ以上余計な制約条件(拡張)が付くと、厳密解を計算するのはほぼ絶望的になってきます。
本研究でやったこと
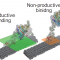
本研究では、ASEPの中でも比較的解きやすい周期境界条件を課した場合について、図に示すような粒子の移動(同じサブシステムから出ていく際には同じ確率レートで出ていく)についてはどんなネットワーク状につないでも、厳密解が求まることを示しました。これによって、複数レーンのASEPや粒子脱着を含むASEPといった応用上非常に重要な拡張について数理的な基礎を与えることができました。

図2. (a) 詳細つり合いネットワーク.特殊な場合として(b)に示すようなASEP全体が粒子浴につながれている場合や,(c)ASEPが複数並行につながっている場合,(d)単一のサイトがランダムにつながった場合といった例を含んでいる.