分子を大きくして渋滞解消!ミクロとマクロをつないでセルロースの酵素分解メカニズムを解明
[紹介論文] T. Ezaki, K. Nishinari, M. Samejima, and K. Igarashi (2019) Bridging the micro-macro gap between single-molecular behavior and bulk hydrolysis properties of cellulase. Physical Review Letters 122: 098102
[論文URL] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.122.098102
はじめに
この文章は、先日我々が発表した論文” Bridging the Micro-Macro Gap between Single-Molecular Behavior and Bulk Hydrolysis Properties of Cellulase”に関する紹介・解説記事です。東大からのプレスリリースにもそれなりに詳しくは書いたのですが、もっと一般向けに、あるいはプロ向けに自由に書きたいことを書いてみたいと思います。ちなみに今ご覧になっているこのウェブサイトは私が研究者や学生向けに作った論文解説記事プラットフォームサービスで、よろしければこれをご覧の皆様にも、こんな感じで(あるいはもっと自由に)使ってもらえると嬉しいです。
本記事ではまず問題の背景や何を明らかにしたのかを分かりやすく説明した後、この研究がどういう風に進んでいったかなどの裏話的な内容も少し書いてみたいと思います。
論文の内容について
背景
皆さんはセルロースをご存知でしょうか?植物の細胞壁(あるいは植物の繊維)を作っている物質で、自然界にかなりの量が存在している炭水化物です。このセルロースというのはブドウ糖がたくさん連なってできています。この自然界に沢山あるセルロース(例えばその辺に生えている草とか木とか)をじゃんじゃんブドウ糖に変えてしまうことができれば、バイオ燃料を作ったりバイオプラスチックの素材にしたりできて資源としてとても役に立ちそうです。しかし、それには大きな障害があります。それはこのセルロースがめちゃくちゃ「硬い」(安定している)ということです。木でできた家とか机とか想像していただければわかりやすいのですが、自然にある素材で、硬いし平気で何十年も保ちますよね。なんでこんなに硬いのかというとそれはセルロースが図1(a)のような結晶構造をとっていて、ギチギチに固まっているからです。なので、普通に分解しようとしてもなかなか分解されてくれません(高温・高圧・強酸性の条件を用意すれば化学的に分解することは可能ですがとてもコストがかかります)。一方、自然界によく目を向けると木を分解しているやつらがいることに気づきます。それは木材腐朽菌と呼ばれる微生物達です。彼らは酵素「セルラーゼ」によって木のセルロースを分解し、栄養にしているのです。この方法なら常温・常圧・普通のPhでも分解ができるので、これを利用したセルロースの分解手法が注目されています。
ただ、このセルラーゼを使った分解反応、反応はしてくれるのですが、なぜか反応が非常に遅いということが知られています。なぜこんなに反応が遅いのか、という謎は今まで研究者たちを悩ませてきました。この反応が他の普通の化学反応と違うところは、セルロース結晶の表面上で起こる触媒反応であること、そして酵素の一つ一つに無視できない大きさがあって、お互いにぶつかり合うこと、です。こうした酵素同士の物理的な接触がたくさん起こるような反応についてはまだまだ分からないことがたくさんあるのです。
このタイミングでこの酵素(セルラーゼ;TrCel7A)がどのようにセルロースを分解しているか紹介しておきましょう。セルラーゼには二つのドメイン(機能的なまとまり)があります。一つはセルロース結合性ドメインともう一つは触媒ドメインです。酵素分子はまず(その名の通り)セルロース結合性ドメインを使ってセルロース表面にくっつきます。そして次に触媒ドメインがセルロースの糖鎖の一本をがっちり掴みます。ここまで結合が完了した酵素は、前に進みながら鎖をバチバチっと切っていってセロビオースという糖を生成します。ちなみに反応が一回起こると酵素が一つ前に進むので、反応の速度と、酵素の「交通量」は同じ量になります。上記のセルロース結合性ドメインによる結合と触媒ドメインによる結合は、ついたらつきっぱなしではなくて、外れたりもします。したがって上記を正確に述べると、まず酵素はセルロース結合性ドメインを使ってセルロース表面でついたり離れたりしていて、そのうち一部の酵素が触媒ドメインによる結合に成功して、反応を始めることができる。分解反応中の酵素も結合が外れてセルロース結合性ドメインの結合に戻る、という形です。
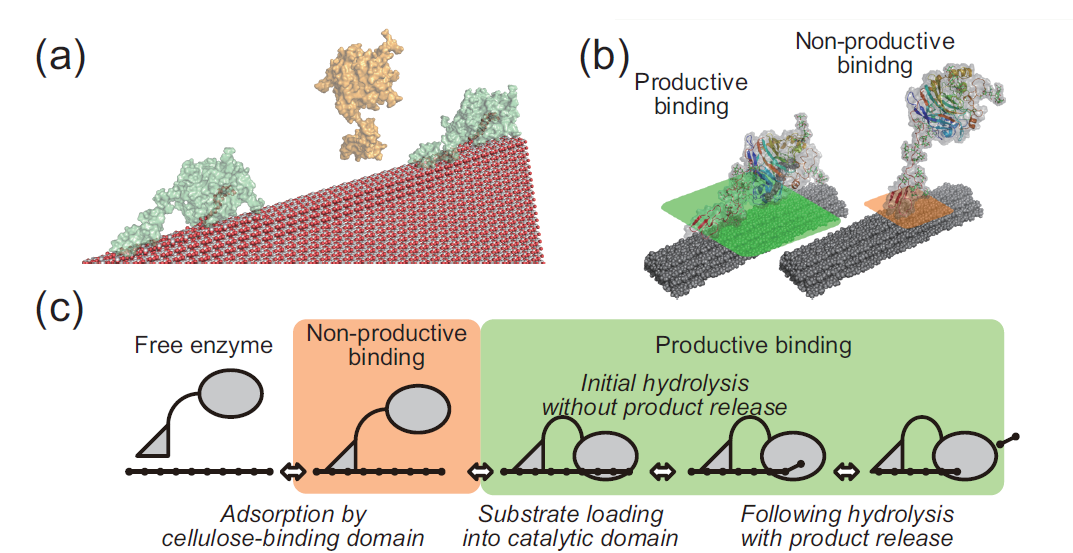
図1.セルラーゼによるセルロース結晶の分解メカニズム
Youtubeに面白い動画があったので載せてみます。若干不正確な表現もあるように思いますが、見やすいと思います。
今回一緒に研究を行った東大農学部の五十嵐先生のグループはこの酵素のふるまいを様々な角度から調べられていて、2011年に「酵素が渋滞している」ということを実験的に測定した論文をScienceに発表されています。この「渋滞」が反応速度低下の原因(のすべて)なのでしょうか?私がこの研究を始めた当時所属していた東大の西成研究室では「渋滞学」という枠組みで様々なモノや人の流れの集団現象を研究していました。そこで五十嵐先生のグループと我々のグループで、より現象の本質に迫れるのではないかということで共同研究が始まりました。
この速度低下の謎で特に興味深いのが、一分子計測の結果とマクロな生化学実験の結果の不整合です。今回研究の対象としたセルラーゼTrCel7Aは希薄条件下、つまり酵素分子の間での邪魔しあうことがほとんどない条件だと、1秒間に7回ほどセルロースの鎖を分解してくれることが分子レベルの測定で分かっています。一方、生化学実験の結果からは、ある程度混雑した条件ではセルロースの表面に存在するセルラーゼ分子の平均分解速度が1分間に約1回ということが分かっています。もしも一分子計測の結果がそのまま使えるならば、酵素分子は1分間に420回反応するはずなので、単純に400倍もの速度差があることになります。しかもこれは反応速度が最大になる条件下で、なのです。渋滞の常識から考えてもこれはかなりあり得なくて、流量最大時の平均速度というのは車の渋滞ならば一台一台の車の速さに一致しますし、確率的に粒子が流れていく模型である非対称単純排他過程(ASEP)では平均速度は粒子の速度の半分です。これらは1次元の流れである一方、セルロースの表面上で起こる反応は準1次元(横同士の相互作用もある)なのでそれが影響を及ぼしているかもしれないということは考えられましたが、調べてみるまではわかりません。ほかにも、この酵素反応では時間が経つにつれ(反応物がなくなるから、ではなくて、反応物はたくさん残っているのに)反応がだんだん遅くなるという現象も知られていて、これも諸説あったものの謎のままでした。また、応用的な視点からは(というかたぶん普通の研究者たちはそちらの方が先に興味があると思うのですが)どういう酵素を作れば反応を速くすることができるのかわかると非常にうれしいです。本研究では、これらの謎たちをすべて解決する理論を提唱しました。
方法
今わかっているのは酵素1分子がどういう風に動くか・そのそれぞれのプロセスの速度を測定した結果と、マクロな生化学実験で得られた反応速度の結果です。わかっていないのは酵素分子たちがたくさんセルロースの表面にやってきて、集団的にどう振る舞ってその結果どうなるか、です。このミクロとマクロをつなぐ、という考え方は物理では統計物理学の神髄であって、その文脈で粒子の集団的な現象を調べた研究がたくさんあります。そこで取られる典型的なアプローチは、モデル化して理論計算and/or数値計算する、というものです(物理一般に言える話かもしれませんが)。今回もそれに従い、この酵素の動きをする粒子を定義してそれを実際に動かしてみました。作ったモデルは以下の通りです。割としっかり長々と書いてしまうので、細かいことにあまり興味のない方は「実際の酵素と同じ動きをするシミュレーターをつくったのだな」という理解で飛ばしていただいて構いません。
今回作ったモデルを動かしている様子。上の動画と比べると些か物足りないようにも思えますが、シンプルなのが大事です。また、こちらの方が最近のエビデンスに基づいて作られているので、正確です。
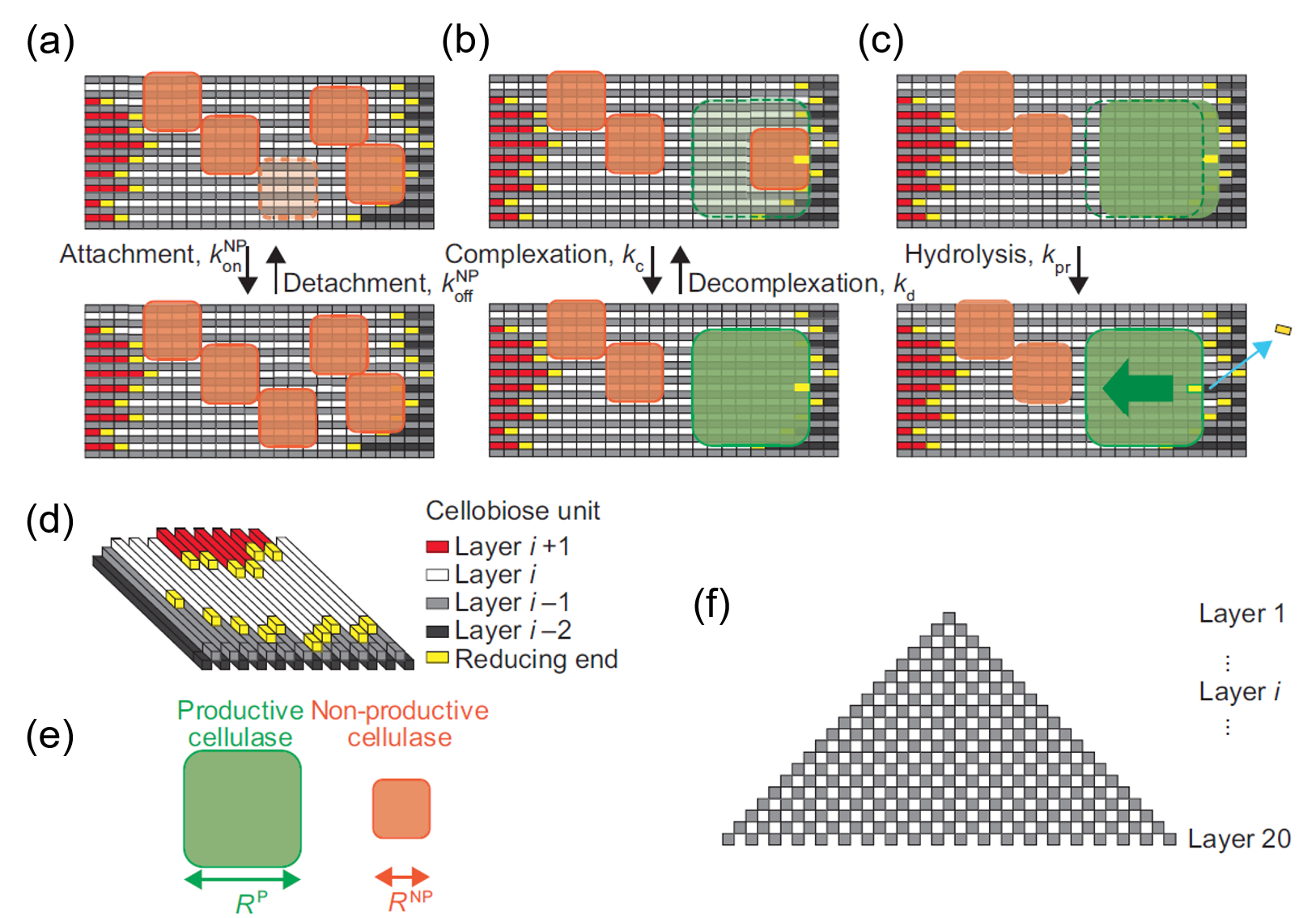
図2.今回作成したモデル
- セルロースについて(図2(f))
分解されるセルロース結晶ですが、実験で使用されるものと整合するように上の図(g)に示すような結晶構造を仮定しました。一本当たりL個のセロビオース分子からなる鎖が20×20の400本、互い違いに並んだ構造です。セロビオースの単位は長さ1nm、幅0.5nmとします。尚、この結晶は同時に上からも下からも分解されるので上半分だけ考えます。
- 酵素について(図2(a-e))
酵素はレートk_on(レートについては後述)で確率的にセルロースの表面にやってきてセルロース結合性ドメインによる結合を試みます。そのくっつこうとした場所に邪魔するもの(この場合、他の酵素分子やセルロースナノファイバーの段差)がなければくっつきます。この結合だけでは分解反応しないのでこれを非生産的な結合(nonproductive binding; NP)と呼ぶことにします。この非生産的な結合はレートk_offで確率的に外れます。セルロースの鎖の端っこ(還元末端)にいる非生産的な酵素は邪魔するものがなければレートk_cで触媒ドメインによる結合に進みます。こうなると晴れて反応を開始することができます。この結合を生産的な結合(productive binding; P)と呼ぶことにします。生産的な結合をした酵素は前に邪魔するものがなければレートk_prで前に進みながら元居た場所のセロビオースを結晶から分離(シミュレーションでは消滅)させます。生産的な酵素はk_dで非生産的な酵素に戻ります。
上記のレートについて説明します。読者の方によってわかりやすい表現が違うと思うのでいくつか書いてみます。ある現象の発生レートがkだとします。すごく簡単に言うと、その現象が起こる速さを決めるのがkで、大きいほど速いです。もう少し説明すると単位時間(例えば1秒とか)で平均的にそのイベントが起こる回数を、出た目を平均するとkになる特殊なサイコロで確率的にきめるということです。厳密な定義では微小時間dtの間にそのイベントが起こる確率がkdtである、という意味です。要するにポワソン過程です。別の言い方をすれば単位時間にその現象が起こる回数は平均=分散=kの正規分布に従うように確率的に動かす、とも言えます。
このモデルでここが一番大切(だと後でわかるのですが)なのが、酵素の大きさです。本研究では非生産的な結合時の酵素の大きさをR^NP、生産的な結合時の大きさをR^Pと定義します。
以上のモデルについて、パラメータをk_pr=7, k_off=1, k_c=0.1, k_d=0.1, R^NP=4, R^P=8と決めます(尚、単位は省略して書きますが、レートに関してはすべて1/sec、大きさに関してはnmです)。これらは一分子計測の研究で得られた値に基づいて(四捨五入的に)ざっくりきめたもので、パラメータ自体はたくさんあるのですが、自由に動かせる値はほぼ無いです。一応、値が多少ぶれても本研究の結論には影響ないことを確かめています(詳しくは論文の付録をご覧ください)。尚、k_onは酵素がセルロース表面にやってくるレートですが、これは酵素の濃度を決めるパラメータになります。生化学実験でも様々な濃度について反応速度が調べられているので同じようにこのパラメータも色々変えて様子を見てみたいと思います。
結果
・モデルの妥当性
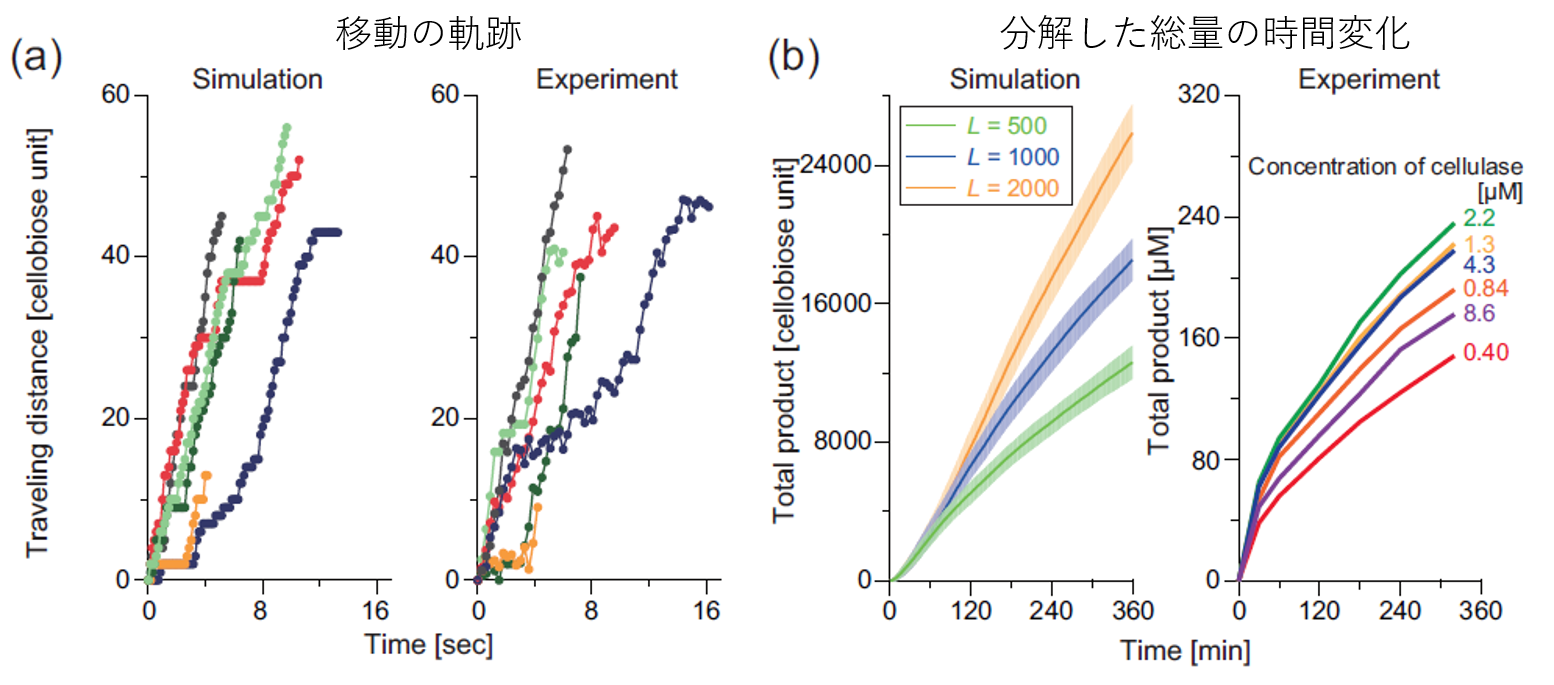
図3.モデルによるシミュレーションと実験結果の比較(1)
最初に、我々のモデルを使って、1分子実験および生化学実験の結果を再現できるかを確かめていきます。結果だけ知りたい方は、我々のモデルが既存研究の実験をよく再現することができた、ということだけ押さえていただければOKです。
まず、希薄条件下(k_on=0.1)で反応を開始した粒子の動きの軌跡を見てみます(上図(a))。横軸が時間で縦軸が移動した距離です。(余談ですが、交通流の文脈ではこれを「時空図」と呼びます。)ExperimentとあるのはIgarashi et al. Science (2011)で報告されている実際の粒子の動き、Simulationとあるのは我々のモデルで得られた典型的なサンプルです。定性的に概ね同じような動きをしています。1分子の情報から作ったモデルで1分子の動きを追跡しているので、ここが合うのは比較的自明ですが、まずは我々のモデルがミクロな振る舞いをしっかり再現していることがいえました。
次に、反応生成物の時系列変化を見ます(上図(b))。横軸が時間で縦軸がそれまでに分解した量です。だんだん反応速度が低下する様子を定性的にとらえることができています。(なぜここで実際の分解された量を定「量」的に比べないのか:今回の反応はセルロース表面でおきるため、その反応速度がセルロース結晶の長さ・太さに大きく影響します。同じセルロース結晶1gでもその分布によって面の大きさ、数が大きく異なります。この分布を正確に知ることは現状難しいので今回はこの比較を行いませんでした。)この結果はシステム全体における反応量の数時間にわたる反応の変化を再現した結果である、といえます。
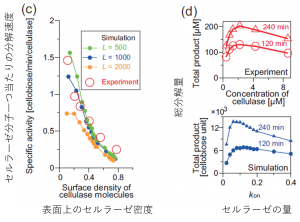
図4.モデルによるシミュレーションと実験結果の比較(2)
次にいよいよ、一番の謎であった分解速度について見てみます。ここでは、セルロース表面に存在するセルラーゼ分子一つあたりにどれくらいの速度で分解するかという量を見ます。また、比較のため、表面上がどれくらい混雑しているか(酵素の吸着可能な最大数から算出)で条件を合わせます。すると、上図(c)の通り、見事にこの強烈な速度低下を説明することができました!これは酵素の数時間単位の集団的な振る舞いのうち1分子あたりの動きを正確に再現した結果といえます。(尚、先ほどは定量的な比較ができなかったのにここではできているのは、これが面当たり・酵素分子当たりの規格化された量だからです。)
最後に、酵素の量を変えたときに総分解量がどう変化するかを比較します(上図(d))。このシステムでは酵素を増やせば増やすほどいい、ということは無くて、むしろ入れすぎると反応が遅くなるという「渋滞」に非常に似た現象が起きます。我々のモデルはこの混雑によって速度が低下する様子もうまくとらえられています。これは数時間単位の酵素のマクロな働きを再現した結果となります。
以上、四つの比較で毎回「この結果は…を再現した結果といえます」ということをくどめに書きましたが、まとめると我々のモデルは、秒単位~時間単位という全ての時間のスケールで、また一分子~システム全体という全ての空間スケール・物質量スケールでも、一分子計測・生化学実験で得られた結果と整合していることになります。このような様々な角度からすべての実験結果を説明する理論・モデルはこれまでに存在しませんでした。
・詳しく見る
モデルがある程度正しく現実を反映しているということを認めることにしましょう。実際の酵素を使った実験と異なり、このシミュレーションの中ではすべての酵素・セルロースの状態を正確に測定することができますし、酵素の特性(パラメータ)を仮想的に変えて反応がどうなるかをシミュレートすることもできます。この、「モデルの強み」を生かしてこの分解過程で何が起きているのかを見てみましょう。
(1)反応速度の低下について
先ほども言及しましたが、このセルロースの分解反応では、反応がだんだん遅くなるということが実験的に知られていますが、それがなぜなのかは不明でした。これは最初に紹介したシミュレーション結果(図3(b))でも再現されていましたね。より詳細に調べるため、セルロースの各層がどれくらいの速さで分解されているのかを測定しました。すると上の層ほど、また左右の境界に近いほど速く分解されることがわかりました。これはセルロース結晶表面の幅が大きくなるにつれて、酵素の混雑が二次元的な配列になり、非生産的な酵素がより邪魔になる頻度が増えることによって説明できます。実際に、幅が変化しないような条件でシミュレーションを行うと速度の低下は起こりませんでした。
したがって、速度の低下を起こさないようにするためにはあるいは反応速度を上げるためには細いセルロース結晶を使えばいい、ということが分かります。(そういったものを用意するのがコスト的に現実的かは別として、ですが一つの知見として。)
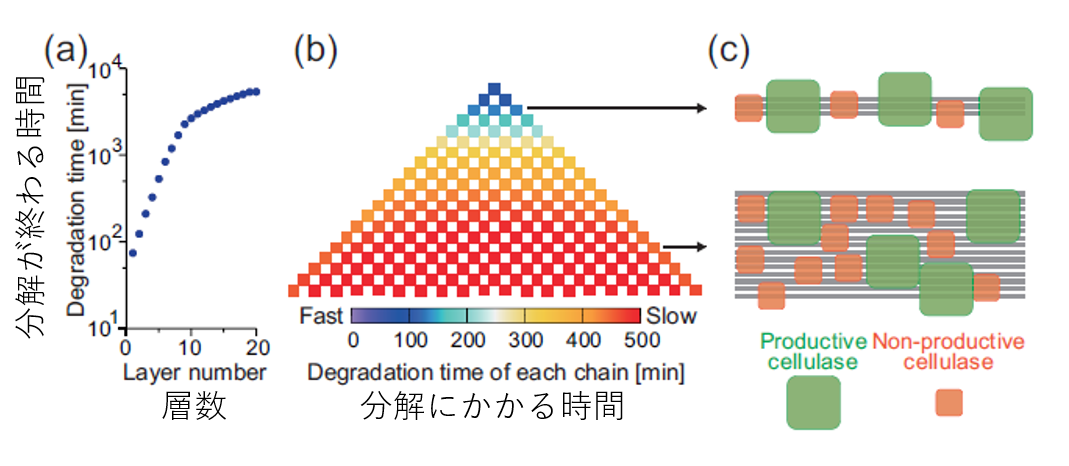
図5.セルロース結晶の各層の分解時間
(2)そもそもなぜ反応が遅いのか
最後に、ここがクライマックスですが、酵素のパラメータを色々変化させてみましょう。設定したパラメータのそれぞれ一つ選んで、値を二倍にしたものと半分にしたものを用意し、様々なセルラーゼ濃度条件で反応速度がどうなるかを見ました。動きに関係するレートを変化させると、反応速度はそこそこの変化をしますが(ちなみに、単に動く速さk_prを二倍にしても反応速度は全然上がりません)、酵素のドメインの大きさを変化させると反応速度は爆発的に変化します(グラフの縦軸が対数になっていることに注意)。しかも条件によっては酵素をいくら増やしても反応速度が低下しません。いったい何が起きているのでしょうか?
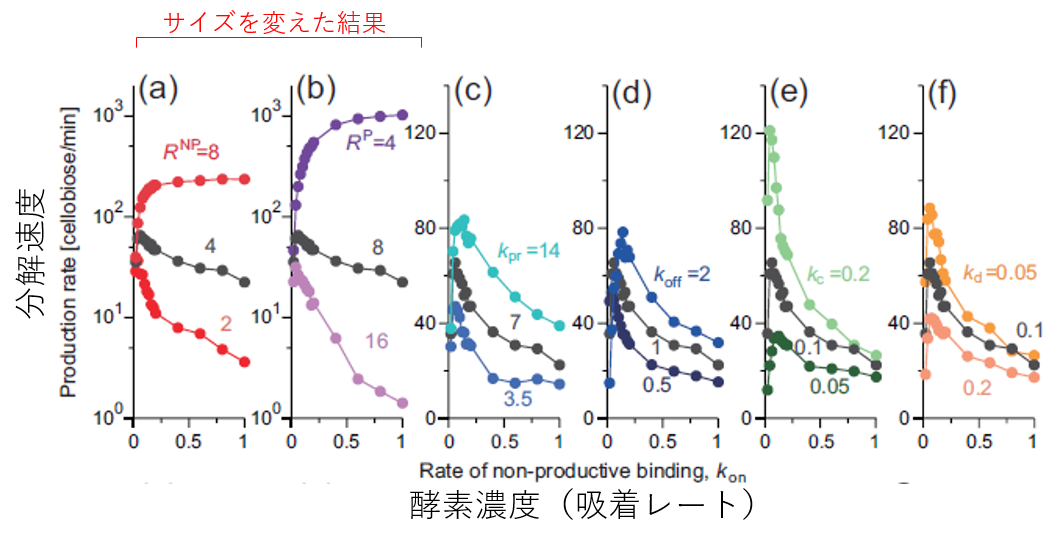
図6.酵素のパラメータ変化が分解速度に与える影響
これを見るため、表面上の生産的な結合をしている酵素の数を数えました。すると、反応速度は単にこの生産的な酵素の数でおおよそ決まっていることが見て取れます。注目するべきは、元の条件(灰色の線)ではセルラーゼの濃度を上げているのに生産的な酵素の数が減っていることです。濃度を上げれば表面上のセルロースの数は増えますから、一見な不思議な結果です。しかしよく考えると、非生産的な酵素の割合がどんどん増えているからだ、という答えに行き着きます(実際そうなっています)。
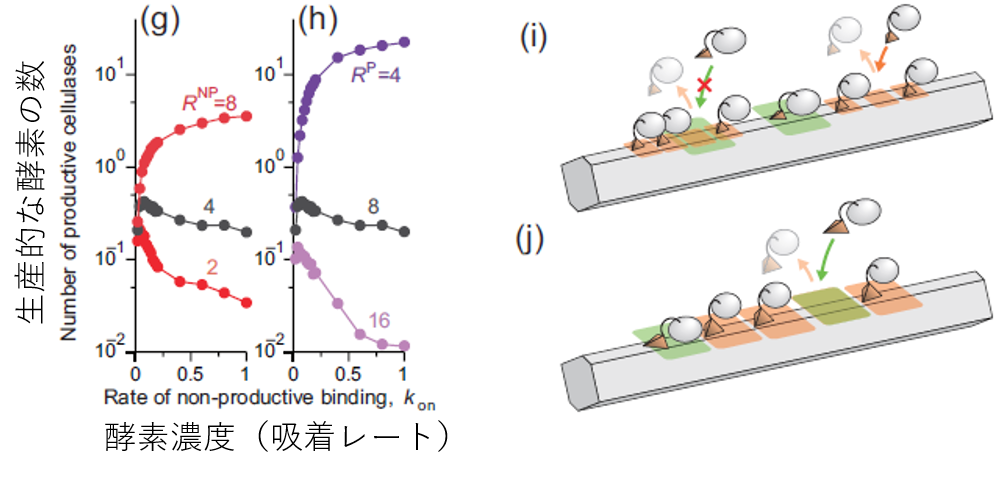
図7.生産的な酵素の数の変化
なぜそのようなことが起こるのか?それはシミュレーションを観察すればすぐにわかります。非生産的な結合は比較的小さい面積を必要としますが、この細かい非生産的な結合が表面上でパタパタ頻繁に起きています。ここに後から大きい面積を必要とする生産的な結合をしようと思っても、非生産的な酵素が邪魔で結合することができません。例えるならば、一人客ばかりのカウンターしかないラーメン屋に5人グループで行って隣同士で座ろうとすることを想像していただくとわかりやすいです。実際のラーメン屋では人が移動してくれたり連続して空くまで席をキープしてくれたりしますが、セルラーゼ分子にはそういった事情は関係ないので5人で順番待ちしていようがいまいが後ろからどんどん抜かしていきます。このような現象のおかげでいつまでたっても生産的な結合に進むことができないのです。(さらにこの5人組には気の短い人がいて、レートk_offで並ぶのを諦めてどこかにいってしまいます)。我々の論文ではこの現象をcrowd-out効果と呼んでいます。
逆説的ですが、一人客にも5席使わせるようにすると毎回客がいなくなるたびに5席が空くので、5人組で来ても一発で座れます。これが我々のシミュレーションで極めて高い反応速度をたたき出しているR^NP = R^Pの条件です。
上:元の条件、下:非生産的結合の大きさを大きくした条件
この発見により、反応速度が速い酵素を作りたいならば「速く動く酵素」ではなく「生産的な結合がcrowd-outされない酵素」を目指すべきであるという新たなパラダイムを生むのではないかと思っています。このためには、セルロース結合性ドメインのサイズを大きくすることや、セルロース結合性ドメインと触媒ドメインの距離を縮めて非生産的な結合時にもっと邪魔になるようにするなど様々な方法が考えられます。
まとめ
- 酵素によってセルロースが分解する様子を再現するモデルを作りました。
- このモデルで様々な角度から実験事実を説明することに成功しました。
- このモデルを調べることによる未知の酵素の集団的な現象が明らかになり、今まで謎だったことがいろいろわかりました。
- 酵素のサイズに注目するべきであるという新たなパラダイムにつながるかもしれません。
裏話・雑感的なこと
論文の内容についてはここまででかなり丁寧に説明を書きました。ここまで来てくださった方ありがとうございます。ここからはこの研究を実施するにあたって経験したことなど自由に記してみたいと思います。意図としてはこういう内容がシェアされていると、研究をやったことのない方々やこれから研究の道に進む学生の方々、他の分野の方々にとって何かの利益になるかもしれない、ということを期待しています。
(1)モデルができるまでの苦労など
この解説や論文を読むと、普通に現実の通りにモデル化してそれでシミュレーションしたらうまくいったのね、とも見えなくはないですが、実際にはここにたどり着くまで膨大な数のボツになったモデル達とシミュレーション結果があります。。この共同研究がはじまって初めてこの酵素の動きを教えて頂いたとき、これは確実に何とかできそうだなと思いました。というのも、このような粒子が確率的に一方向に流れていて、表面に粒子が脱着するようなシステムとしては分子モーターなどで似たような研究がありましたし、当時の私はピンポイントでこの手のモデルにだけ異様に詳しいマニアだったので、何とかできるだろうという自信もあったからです。
というわけで教えて貰った酵素の動きを再現するモデルを作っていきました。物理の基本的な考え方だと思いますが、現象を説明できるならモデルは簡単であればあるほど良いです。というわけで最初は一次元で粒子の大きさは全部一緒で、みたいな単純なものから調べていきました。まずは酵素の濃度が増えると反応速度が落ちる現象の再現を試みました。この記事で言うところの図4(d)の結果です。これは定量的な比較ができない量なので定性的に速度低下が起こるかを見ます。この手のシステムで表面上の粒子の数が増えると流量(=反応速度)が落ちることは渋滞の文脈では実は常識なので比較的簡単に再現することに成功しました。しかしこれは実は逆に罠で、この現象自体は大抵のモデル・システムで見られる現象なので、定性的に再現できたからといってそのモデルが正しいとは殆どいえないのです。途中までは当時作ったモデルでいけるかな、と思っていたのですが、詳しく調べるとその他の実験結果をうまく説明できないことが分かってきました。特にセルロース表面上の酵素粒子一つあたりの分解速度(この記事の図4(c))の値が平気で数十倍ほど異なっていましたし、濃度を上げても減らないしで全然合いませんでした。
そこでいままで正しいと信じていたモデルを放棄して、必要と思われる要素をひとつずつ追加していきました。正しそうな結果が出たのは生産的・非生産的結合の大きさの効果を別々に導入したときでした(結果を見ればここで説明が可能になるのは自明ですね)。この時、上記の酵素一つあたりの分解速度がまともな値になり、また同時に(それまでは直線的な振る舞いしか見えなかった)反応生成物の時系列変化(図3(b))もまともな挙動を示すようになりました。それまでのモデルでは、どんなにパラメータを変化させたとしても出なかったものがいとも簡単にでたので、ロジックではないですが、ここで「あ、これは来たな」と思いました。シミュレーション結果は1つの条件につき2時間分のトライアルを100トライアル計算して平均して算出しているので、それを様々な濃度条件で調べるとなると結構な時間がかかります。これをパラメータをかえつつモデルを変えつつやっていたのでここまで来るのに普通に年単位の時間がかかってしまいました(が、何とか執念でpublicationまでもって来れてよかったです)。
(2)crowd-out現象の物理
この現象自体は二つの大きさの異なる種類の粒子を表面に脱着するようなシステムでは普遍的に出るはずなので、特に新規性はないはずです。ただ、これについては(理論計算がほぼ無理だというのはわかるのですが)本とかにちらっと書いてあるくらいで、この現象についてあまりいい文献を見つけられておらず、このあたりがどうなっているかは把握しきれていません。(どなたかご存知でしたらコメントなどでご教示いただけますと幸いです)。また今回は現実の実験結果の再現を重視した複雑めなモデルを考案しましたが、理論的な解析がしやすい一次元版の系などを考えればexclusion processの物理として多少は調べる意味があるかなとも思っています。
最後に
ここまで読んでくださった皆様、本当にありがとうございました。もしよろしければシェアなどでしていただけますと非常にありがたいです。また、他にも面白い記事が沢山投稿されていますのでよろしければそちらも是非覗いて行ってみてください。それでは!